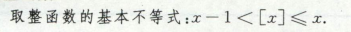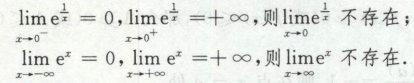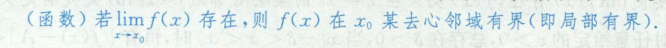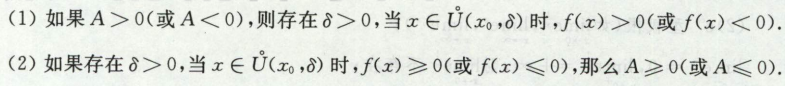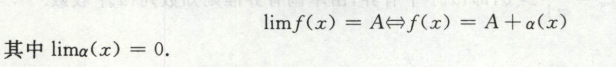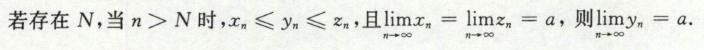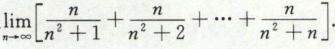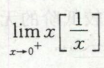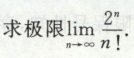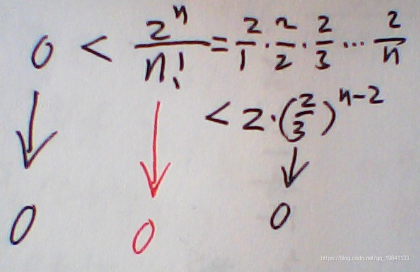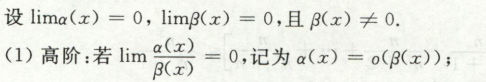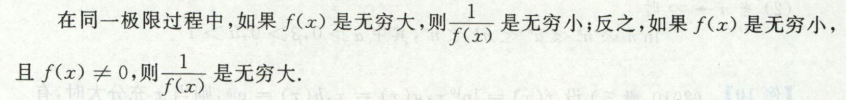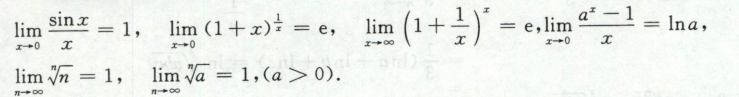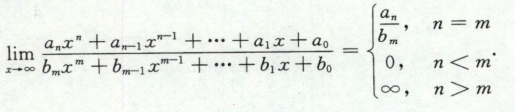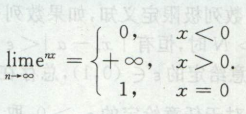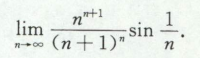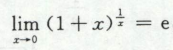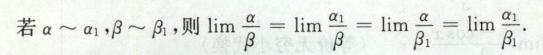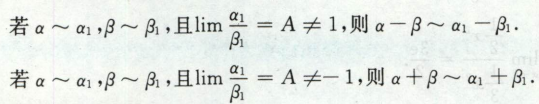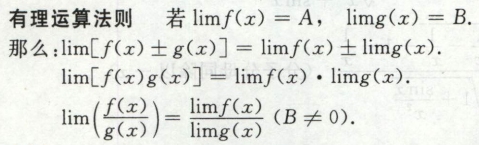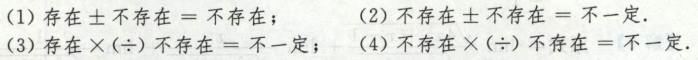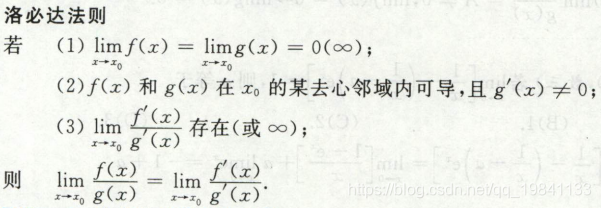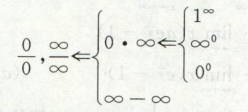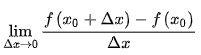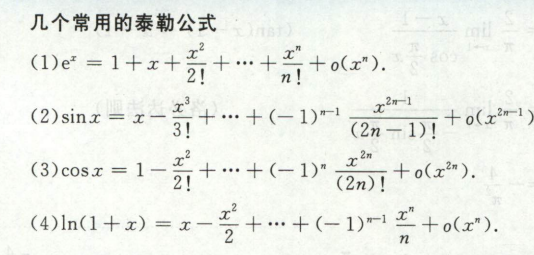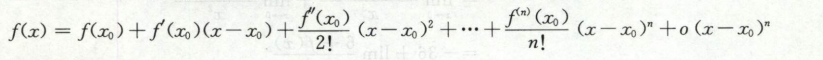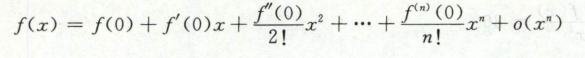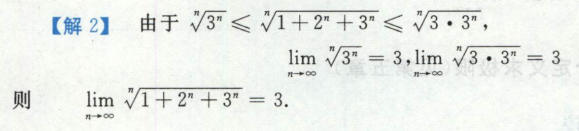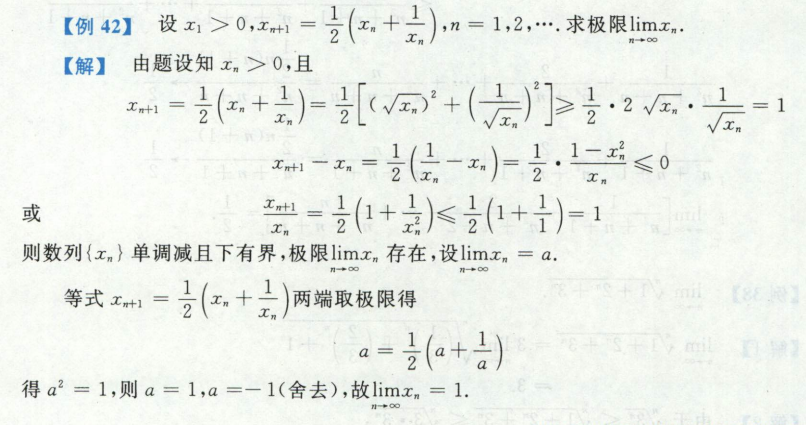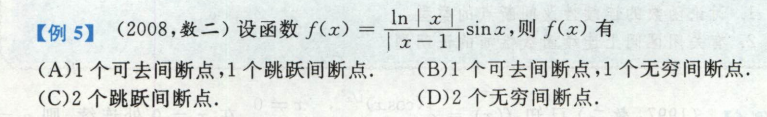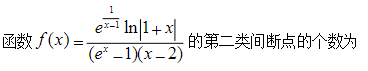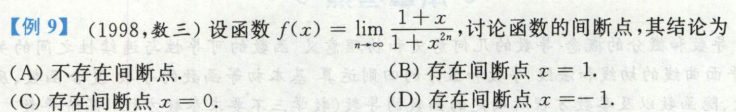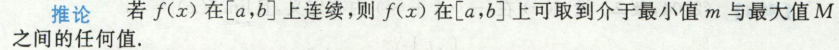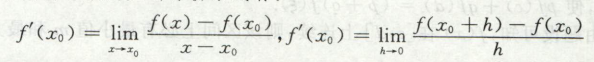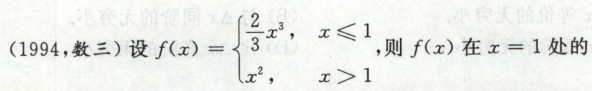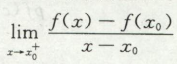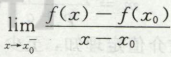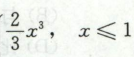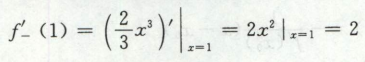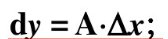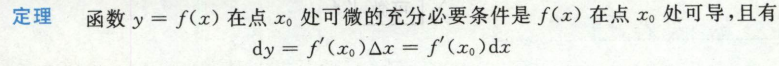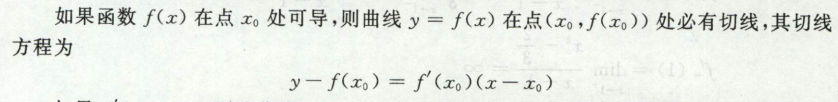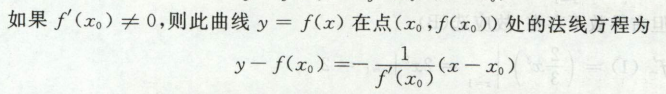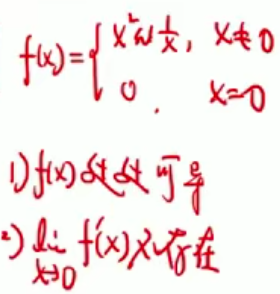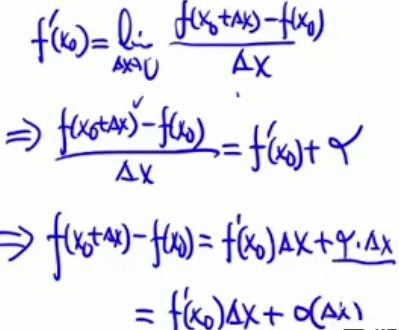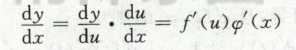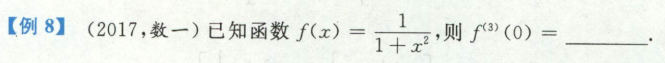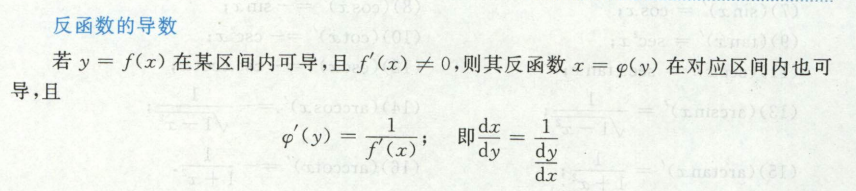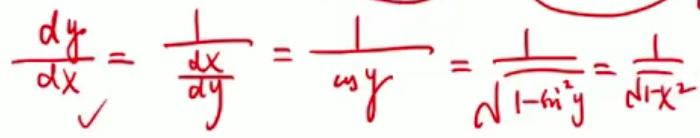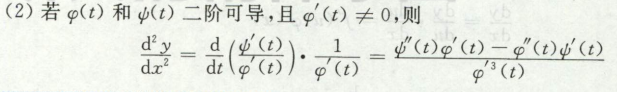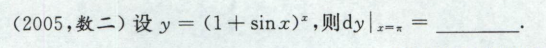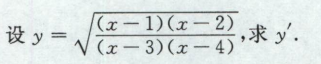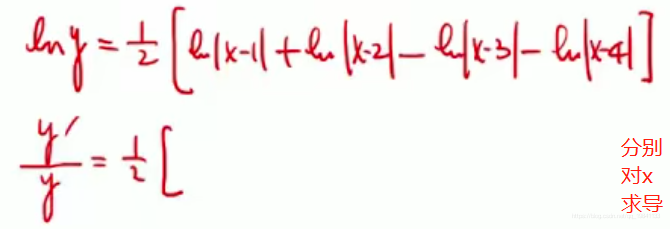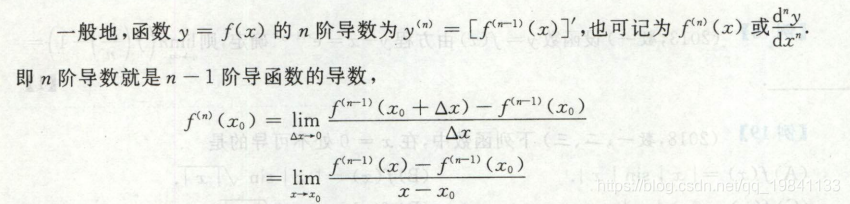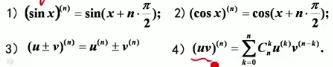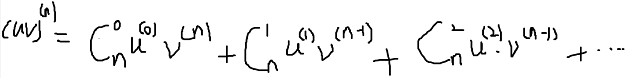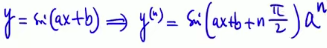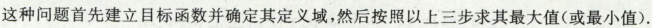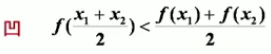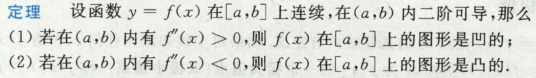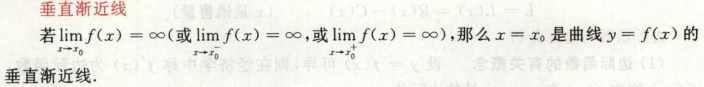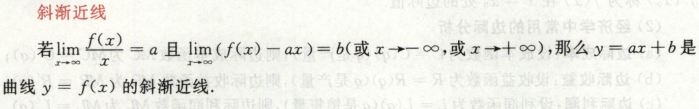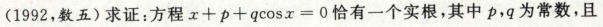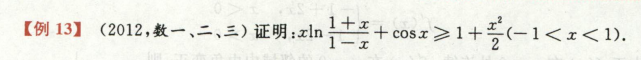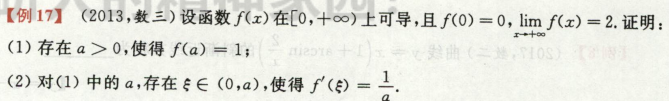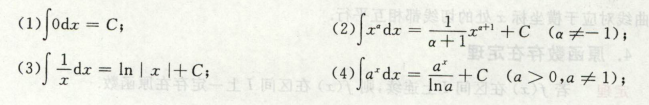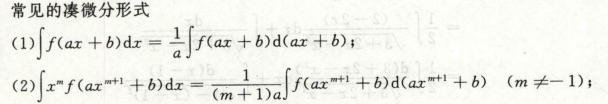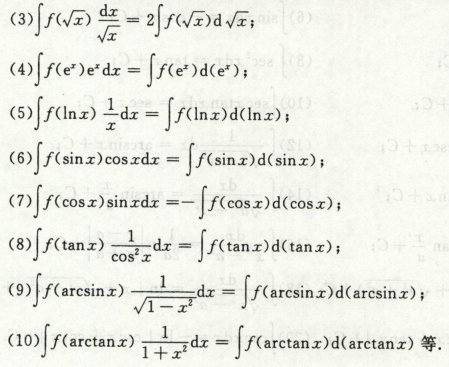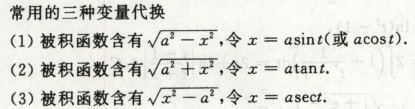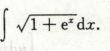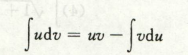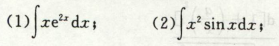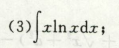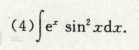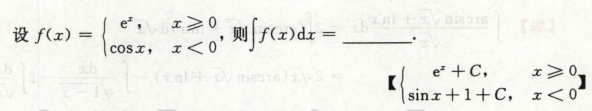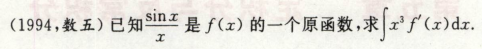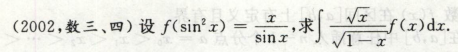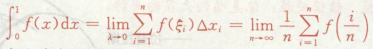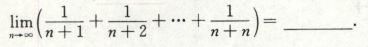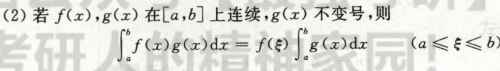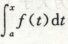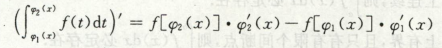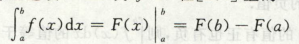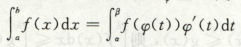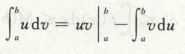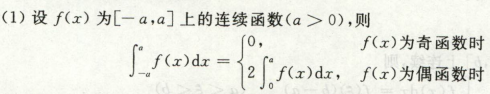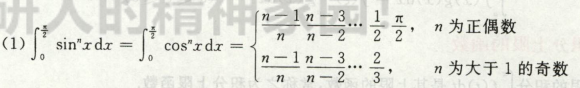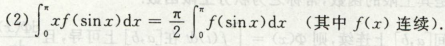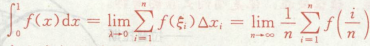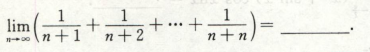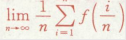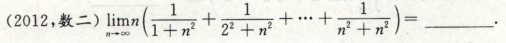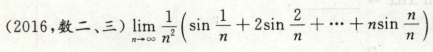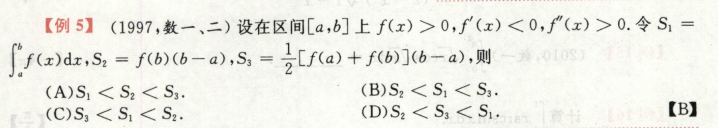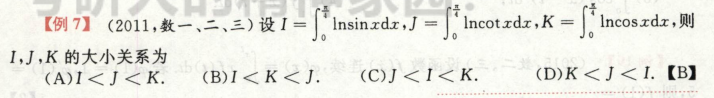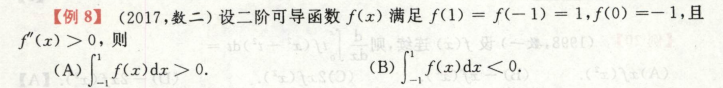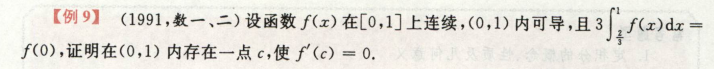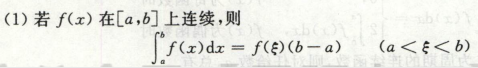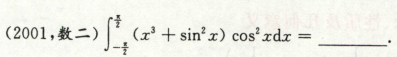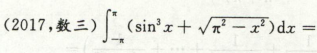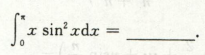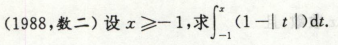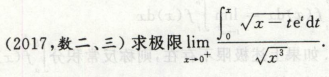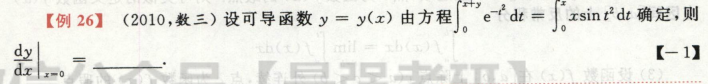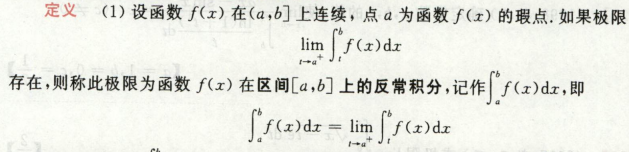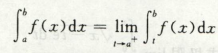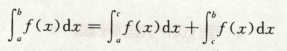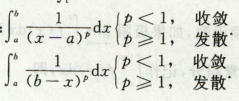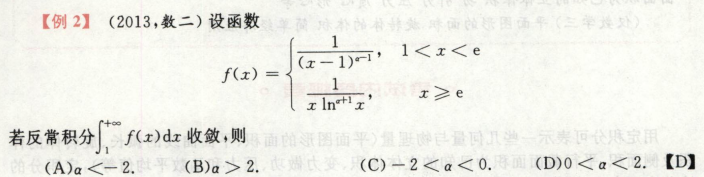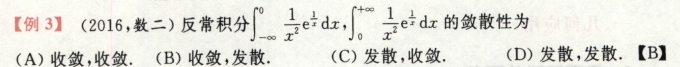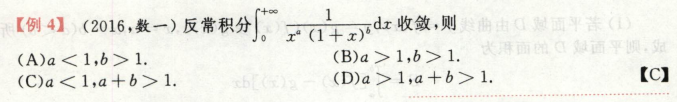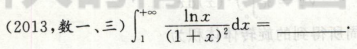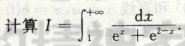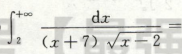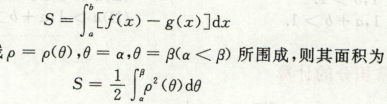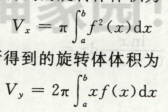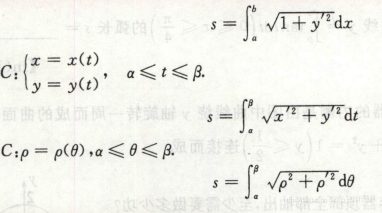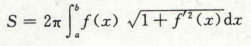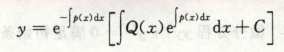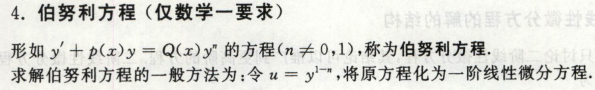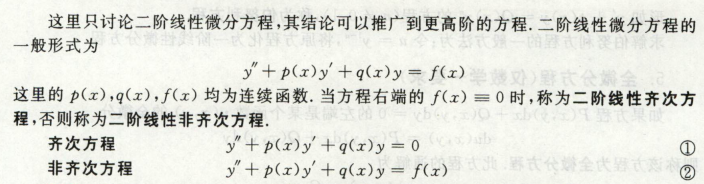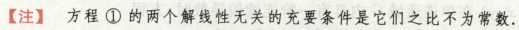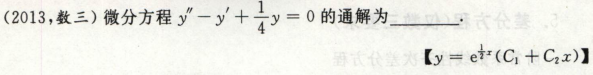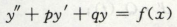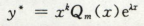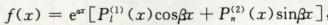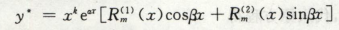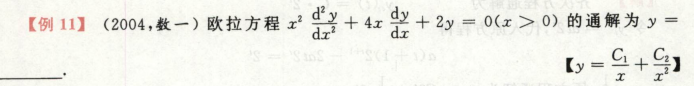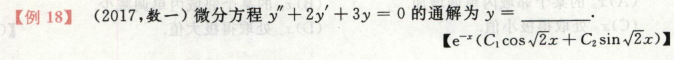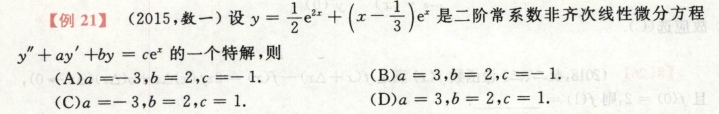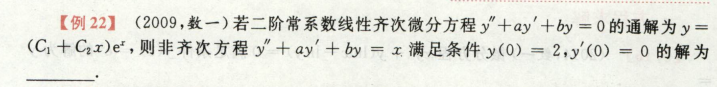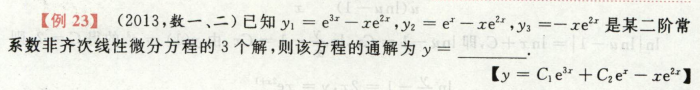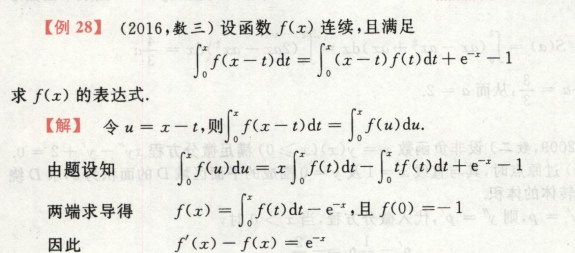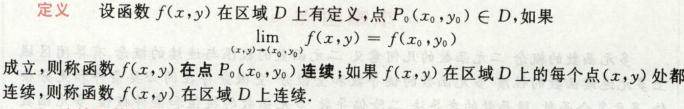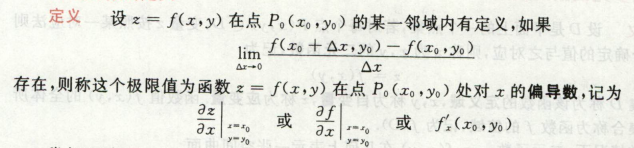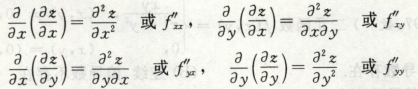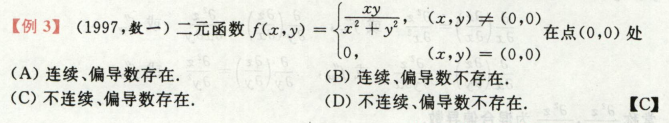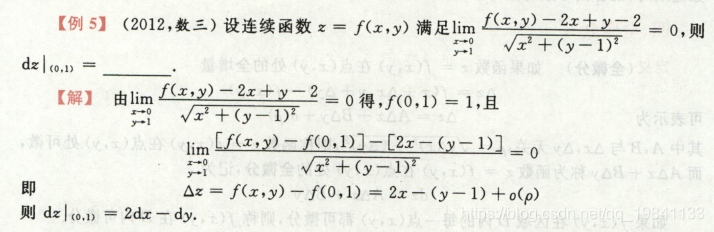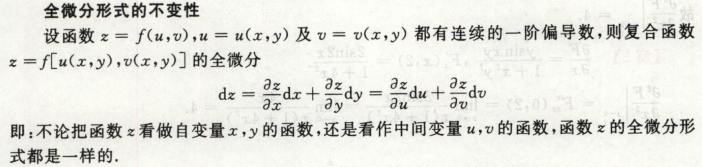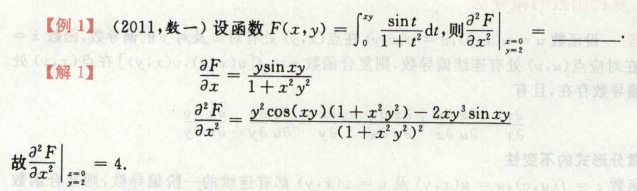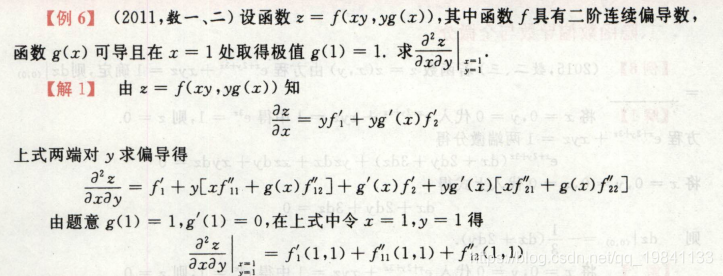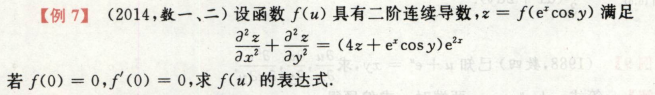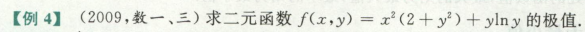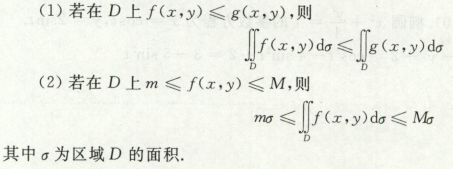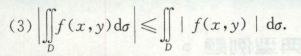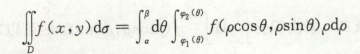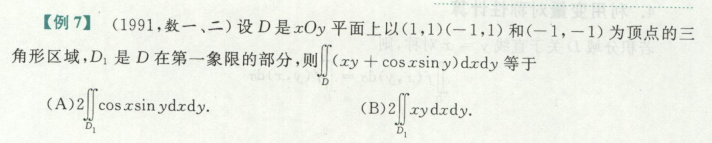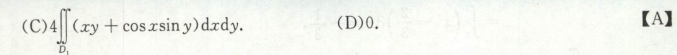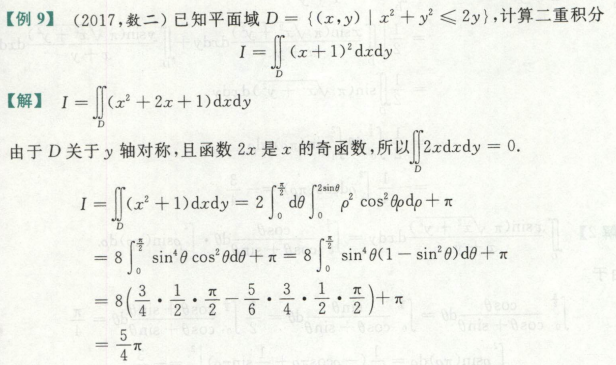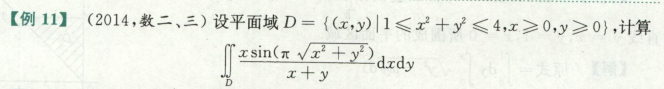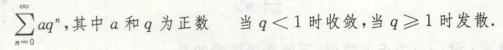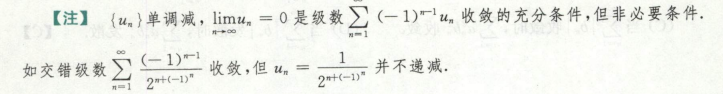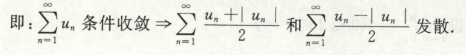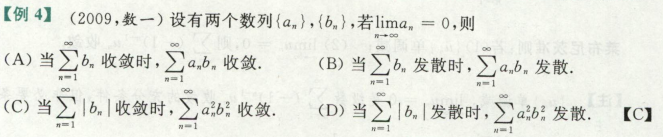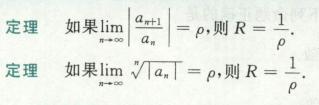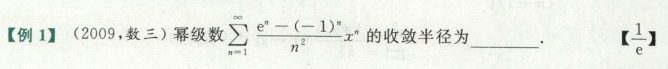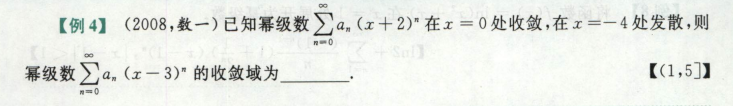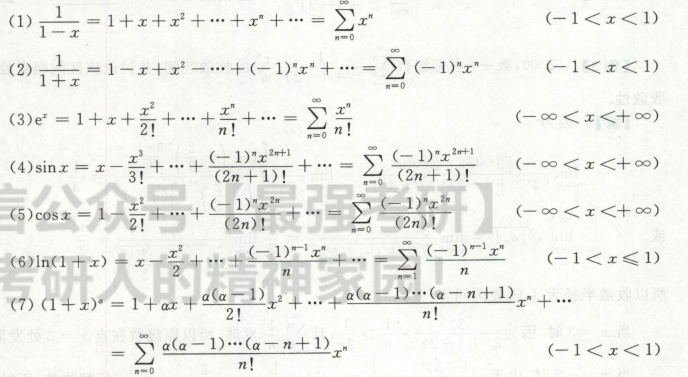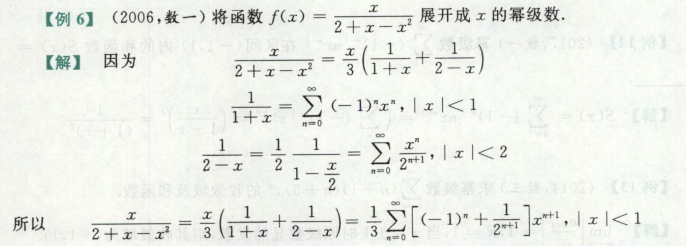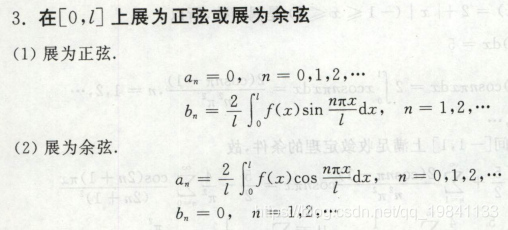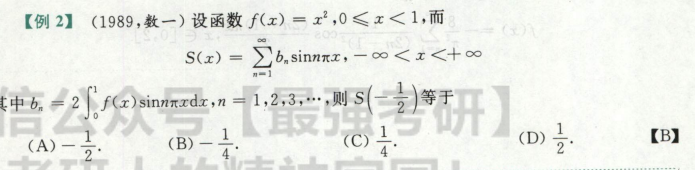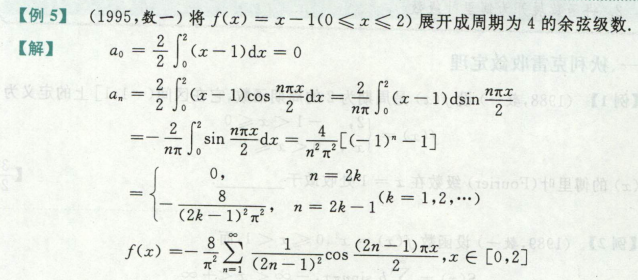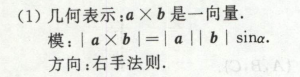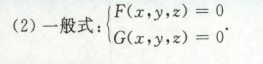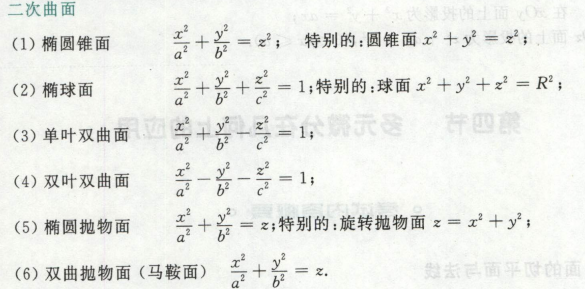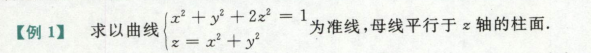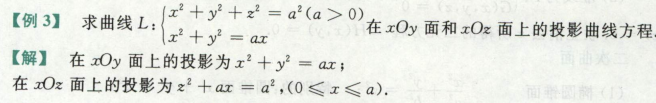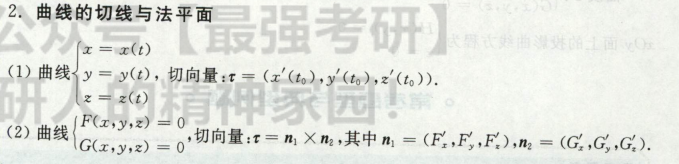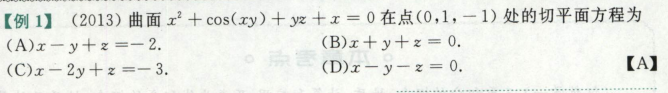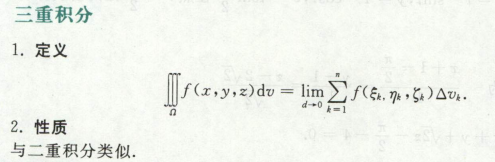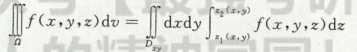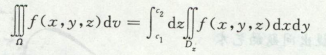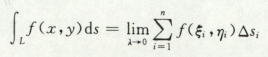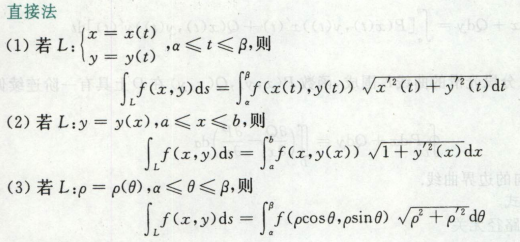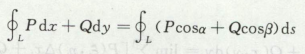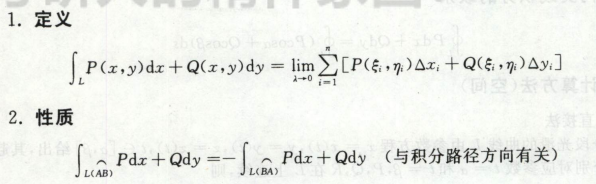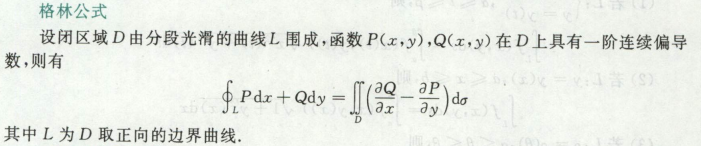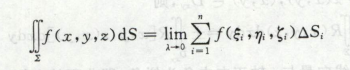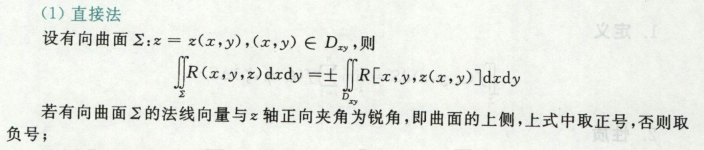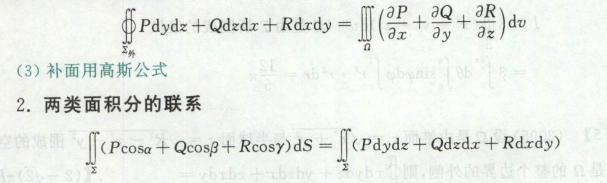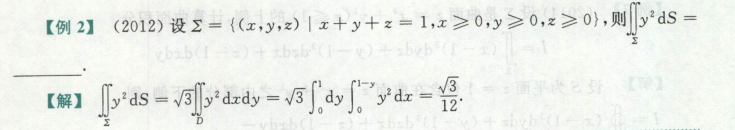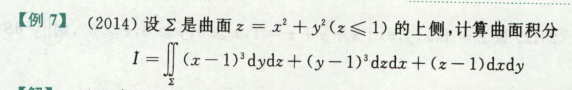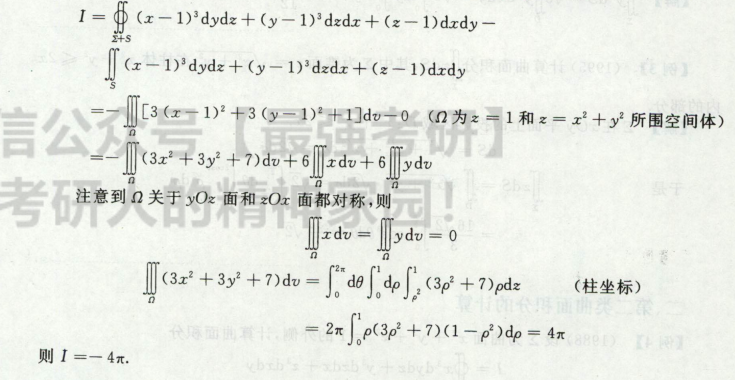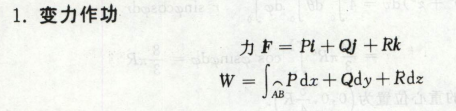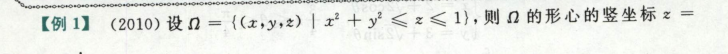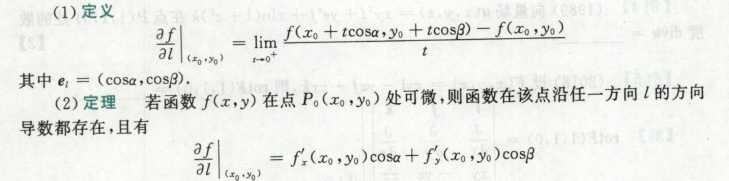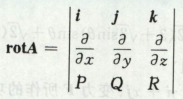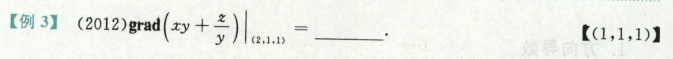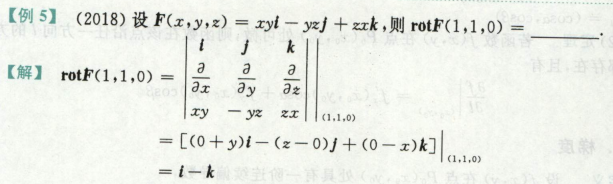高等数学
文章目录
- 第一章 函数 极限 连续
- 第二章 导数与微分
- 第三章 微分中值定理及导数应用
- 第四章 不定积分
- 第五章 定积分与反常积分
- 第六章 定积分的应用
- 第七章 微分方程
- 第八章 多元函数微分学
- 第九章 二重积分
- 第十章 无穷级数
- 第十一章 向量代数与空间解析几何及多元微分学在几何上的应用
- 第十二章 多元积分学及其应用
第一章 函数 极限 连续
函数
取整函数
复合函数y=fg(x)
条件是g的值域∩f的定义域≠空集
反函数存在的充要条件:y有且仅有一个对应的x,如y=x2就没有反函数
函数fx :x映射到y
反函数f-1x : 从y映射到x
求y=shx的反函数,解法:将ex视作整体,分子分母同乘ex
- 初等函数
arctanx
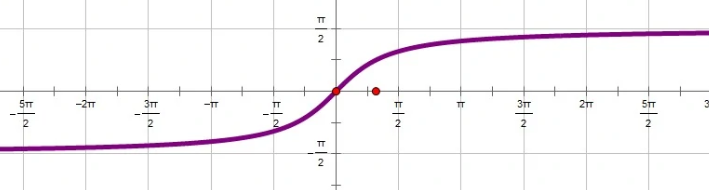
arcsinx
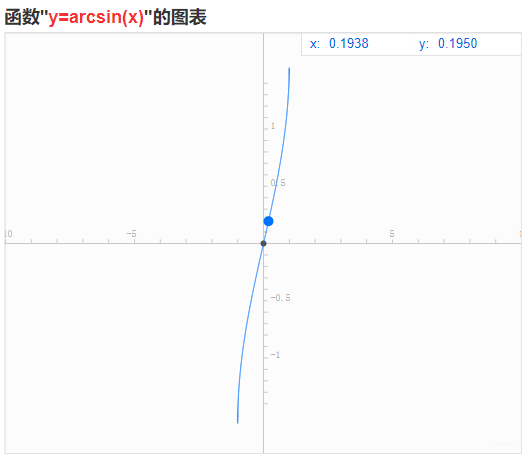
arccosx
奇偶性
奇 + 奇 = 奇
偶 + 偶 = 偶
奇 * 奇 = 偶
奇 * 偶= 奇周期性
sinn(x),n为偶数周期为派,n为奇数周期为2派
如:sin2x周期为派,∫0到派 sin2x dx,区间可以换成0到派/2
sin3x、sin5x周期都为2派
f(x)周期为T,f(ax+b)周期为T/|a|有界性
注意无界函数的定义的有界函数的补集,所以一个函数不是有界函数就是无界函数
注意这里有界是有上下界的,-M<=f(x)<=M
极限
数列极限
xn看作一个是值,落在x轴上的值,同时也是数列中的一个值
数列极限存在,部分列极限也存在
注意:所有部分列能还原成原数列,且所有部分列极限存在且相等才能反推原数列极限
∞在函数和数列中定义是不一样的,数列中无穷默认为+无穷
在函数中:
x -> ∞,要判断两个极限,一个是x趋向+∞,一个是x趋向-∞,左右有别
左右有别的常见考题,x->0,在x=0处出考点
极限性质
有界性
反之不成立,如sin(1/x),在x->0处极限不存在
保号性,注意等号,
limx->x0 f(x)=A存在,则有:
若A大于0,则在去心邻域中fx>0
若在去心邻域fx>0,则A大于等于0,(如fx=x2,在x=0处,去心邻域fx>0,但是A=0)
极限与无穷小关系
夹逼准则
夹逼准则常用在求极限,
那么如何判断这个极限能用夹逼来做?
取整函数
n的阶乘远大于2n,所以等0
这题提一个3出去
单调有界准则
要用这个定理先要证明有界
无穷小比较
高阶、低阶、同阶、等价,k阶无穷小
无穷小性质
注意有限个
无穷大量
洛必达常用,直接看最高阶的项即可
无穷大量性质
两个无穷大量之和可能为0, n + (-n) = 0
数列的无界变量
数列无穷大量举例
无界变量举例
注意 无穷小可能=0,就不能做分母,
如:fx=0,limx->0 f(x) = 0, 1/fx不存在
求极限
常用的基本极限
只用判断最高次项
注意lim a(x)=0,lim b(x)=∞的条件,不是任何条件都可以乱用的!
结论的推导还是用的幂指函数求极限的方法,保守点就用幂指函数求极限
4个讨论点
3个讨论点
例题:
这里用的是
常见等价无穷小 要背 mark
代换原则
相减代换等价无穷小,要求a和b不等价即可,如:sinx - x 不能代换,2sinx - x ~ x可以代换
相加可以看作a - (-b)的形式,这两条是等价的,sinx + (-x) 就不能代换
补充:1-cosax ~ (a/2)x2
注意:等价无穷小做初等公式变换,如(x-sinx)1/2,(1-cosx)3,这些把原来的等价无穷小看作因子,相乘就是幂次形式,所以不要被吓到
这里的等价无穷小可以推泰勒展开,如 1-cosx ~ 1/2x^2就可以推 cosx的泰勒展开,ln(1+x),(1+x)^a的泰勒也可以推了,在稍微记一下通项就基本记住了
有理运算法则
有两个极限存在就能推第三个极限一定存在,注意下面可以拆分的条件是极限A和极限B存在
注意:
有三种组合
【存在 ±*/ 存在 】,这个一定存在
【不存在 ±*/ 不存在】,都不一定
【存在 ±*/ 不存在】,只有存在±不存在=不存在
lim ∞ * x = 常数 可推 lim x一定为0
洛必达,注意洛必达是否可以用,得先求才能知晓(结果是存在或者∞才能用)
七种类型的极限都可以用洛必达法则
∞-∞可以通分用洛必达,也可以直接用泰勒展开
0±0和∞±∞常用泰勒展开,展开原则,展开到x的最高阶
注意化简
如果含有极限非0因子,先求出来,以化简
注意使用等价无穷小只能在乘法因子中使用
如果f(x)一阶可导,没有说连续,那么不能用洛必达法则!
如果f(x)二阶可导,没有说连续,只能洛到一阶。
这种题型使用导数定义做:
常见泰勒公式
tanx用tanx - x ~ 1/3x^3推,1±x的泰勒可用ln(1+x)的泰勒求导得到,arcsinx和arccosx只是sinx和cosx变下号,
补充 (1+x)a = 1+ax + a(a-1)x2 / 2! + …
皮亚诺泰勒公式
特别地,在x=0时
0±0/0
∞-∞/∞
分子就可以用泰勒,一桶刨沙
注意!!! 分子不能用等价无穷小,因为不是乘除法的因子,这里是±
(等价无穷小使用条件是,等价无穷小代换后相减或者相加后不等于0)
夹逼原理求极限
这题其实将3提出来做更简单
重要结论:
单调有界求极限
题型:数列推导求极限题
先要用单调有界准则证明极限存在(首先说明单调增并且有上界=>极限存在),然后才能设limXn=limXn+1=a求极限
单调有界准则 常用不等式证明有界,
这里用的2ab小于等于a2 +b2
补充均值不等式:算数平均和几何平均比较常见
函数的连续性
左右极限等于函数值:lim f-x = lim f+x = fx
区间连续
间断点
第一类间断点
第二类间断点
间断点题型:找有几个间断点,讨论间断点
如何找间断点?找不存在的值处
这个fx函数可以拆成3个因子,每个因子分别找无定义的点处,x=0,x=1处,直接求极限,但是出现ex,arctanx,分段函数,|f(x)±a| 时得分左右极限来求
那这个fx可以拆成4个因子,依次判断无定义的点即可,核心还是求极限
讨论间断点题型:
这一题做了一点变化,这里首先是得求出fx,而求出fx又要x分类讨论
这里考点是4个讨论区间
在讨论x=1处和x=-1处,判断是否间断?判断是跳跃间断还是可去间断?
考点2:关于连续性运算和性质,连续函数的性质的证明题
首先是连续函数的最值定理,存在最大最小值
其次用到了介值定理的推论,f(ξ)应该想到:m<=f(ξ)<=M,所以把证明改写,将p+q移过去,单独把f(ξ)表达出来。
介值定理
第二章 导数与微分
导数的概念
求导,其实就是特殊的极限,因此一阶导可以看作是fx的特殊极限(Δx->0),二阶导可以看作是一阶导的特殊极限。
两种写法,这两种写法分母都是分子的自变量相减
题型:判断导数存在性
这类题有三种方法:
1)左右有别,分别用定义去计算导数,最普遍的方法
2)等号这边的函数,可以用其导函数来求导
如:
那么f’+则需要用到定义去求
3)导数存在的必要条件:此点连续。如果此点不连续那么导数不存在
什么叫连续?连续是指函数在此处极限存在且与函数值相等
什么叫可导?直观来讲,可导就是在这点的上的切线有一定的方向;可导可以看作是fx空心邻域与此处fx值的关系,有空心邻域fx必要条件就是此处连续
从直观上看,
若不连续,导致这点上的导数的切线缺失了方向(变化率不存在,或者说是切线变化不光滑),导数不存在。
更何况连续都不一定可导,譬如fx=|x|
微分的概念
导数是函数某点的变化率,微分是函数的改变量
通俗的说微分是函数上的一小段(用kx拟合)在y轴的映射
dy是Δy的线性主部(近似的主要部分),将Δy的高阶无穷小忽略了
dy=f’x · Δx (1988年考过这个定义,判断dy和Δx同阶,dy/Δx=f’x)
考的定义,dy除以Δx=f’x
可微的(充分)必要条件是可导,就是可微和可导等价,
很少考可微性的判定,因为可微判断可导即可(一元中可微和可导等价),不会用定义去做,而可导需要用到定义去判断。
出题习惯:
一元考导数,多元考微分
导数与微分的几何意义
切线方程
法线方程
微分是函数上的一小段(用kx拟合,简单讲就是切线代替曲线,dy是切线拟合,Δy就是原本的曲线)在y轴的映射
连续可导可微之间的关系
一元中:
可导和可微等价
可导必连续
连续不一定可导(y=|x|,x=0处)
证明:可导 => 连续
可导 => 连续的正确理解,可导和一阶导连续、一阶导极限是否存在无关
反例:
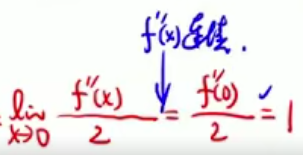
所以,在fx二阶可导的时候,洛必达不能乱用,fx二阶可导且连续才能求到二阶,(注意:二阶可导说明f’x连续;而fx可导是一阶可导,说明的是fx连续)
=>二阶可导,lim f’’(x)不一定存在,更不一定连续,洛必达只能用到一阶,后面请使用导数定义
=> n阶可导,n-1阶导函数连续
证明:可导 => 可微
导数公式及求导法则(背
sec = 1/cos
csc = 1/sin
cot = 1/tan = cosx / sinx
链式求导法
例7做结论:fx为偶函数,f(2n-1)x为奇函数(f’x, f’3x, f5x… )
隐函数求导
反函数的导数
y=arcsinx
x=siny
y’ = 1/x’ = 1/cosy
参数方程求导
对数求导法
但是这个幂指数改写成exln(1+sinx)会好做一些
这题就很适合用对数求导,因为对数可以把乘法化成加法
高阶导数
n阶导数存在 => n-1阶导数存在
常用高阶导数
1)式拓展
相关变化率
这题我们已知x对时间的变化率,求另外一个变量l对时间变化率,这种题型叫相关变化率
x和l是两个相关的量,
首先建立起这两个相关量的关系
题目要求我们l对t求导
使用公式求解:dl/dt = dl/dx * dx/dt
第三章 微分中值定理及导数应用
考题:求极限、极值最值、凹向拐点、渐近线、方程的根、不等式证明、微分中值定理证明
微分中值定理
定理略 P39
什么时候用微分中值定理
题目告诉我们导数的条件,让我们研究函数
或者给的是函数条件,研究导数
泰勒公式
本质是建立fx和高阶导数之间关系
用多项式逼近一般函数fx
导数应用
函数的单调性
函数的极值
极值的必要条件,导数=0
导数=0的点称为驻点,驻点包含极值点(错),极值点(y=|x|)不一定是驻点
如果fx可导的条件下,才极值点=>驻点,驻点包含极值点
因此:极值点 => {f’x=0或者f’x不存在}
极值的第一充分条件
细节,可以用在导数=0处,也可以用在导数不存在的点处只要fx连续
极值的第二充分条件
连续函数在区间的最值
最值要么在内部的极值处,要么在端点处(极值是一个领域,所以极值不能在端点取到,但这里是最值)
解题:
凹凸性
拐点
拐点是曲线上的点,用(x0,y0)表示
渐近线
水平,x趋向±∞,arctanx
垂直,如tanx,分母等于0的点就是可疑的点
斜,±∞的一侧出现斜渐近线
首先求 lim fx/x = a, 再求 lim fx - ax = b
作图
1/定义域
2/一阶导数
3/二阶导数
4/渐近线
曲率
常见考题
求函数极值
f’x=0或者f’x不存在
左右两侧异号
函数连续+保号性
求拐点:
y’‘x=0
y’’左右两侧异号,图像上看一边是凹一边是凸
渐近线
水平:看x趋向∞,fx=常数
垂直:fx=∞
斜渐线:
x->∞,
y/x = a, y-ax=b
fx能够写成ax+b+a(x)的形式
方程的根
1)零点定理,区间连续,fx异号 = > 至少存在一个根
2)构造辅助函数使用罗尔定理,F’x = fx,区间连续,端点相等 => 存在fξ=0
不等式证明
1)单调性,构造函数,求F’x
2)拉格朗日中值定理,使用 a < ξ < b
3)最大最小值
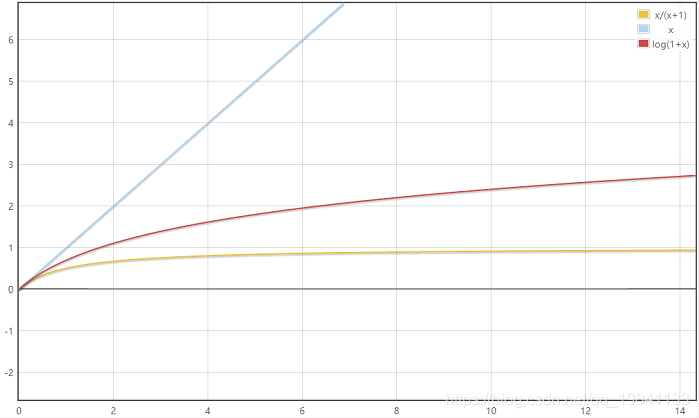
常见结论:
x/1+x < ln(1+x) < x,x>0
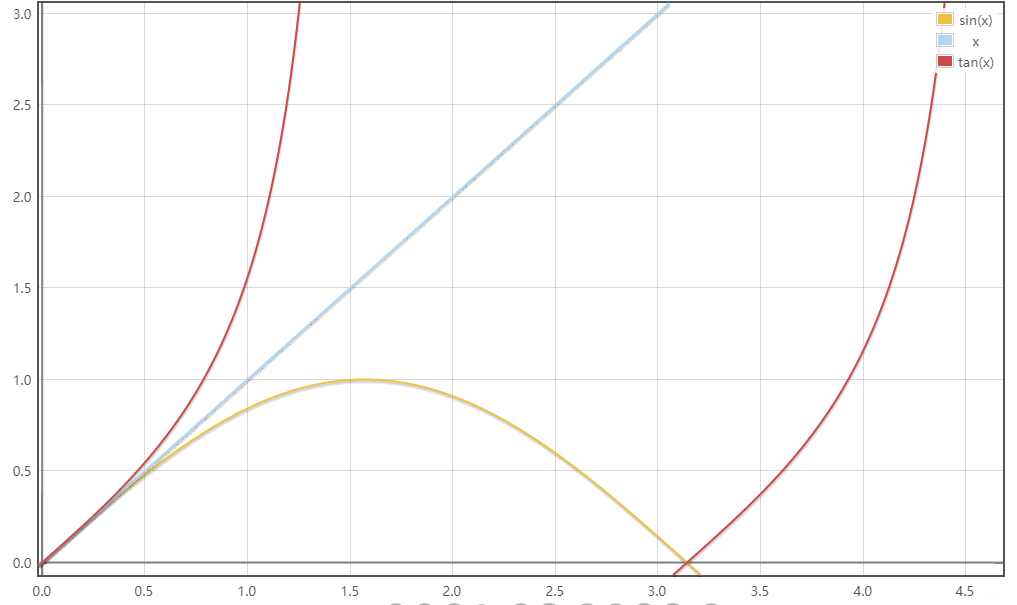
sinx < x < tanx,x∈(0,🥧/2)
2012年考题:
首先考了函数性质:偶函数
构造函数Fx即可
中值定理证明题
1)拉格朗日中值定理
2)构造辅助函数(一般是直接把右边移动到左边),罗尔定理
考了介值定理和拉格朗日中值定理
第四章 不定积分
2+3+3:
2个概念 原函数和不定积分
3种解题方法
3类积分
原函数和不定积分
原函数 Fx+C
不定积分 ∫fxdx=Fx+C
存在原理
但不连续也可能存在原函数
不定积分的性质
d∫与∫d:∫ 1 dg(x) = g(x) + C, d∫g(x) = g(x)
∫ (fx±gx) dx可拆成两部分
∫ k·fx dx常数可先提
不定积分基本公式 (背
secx = 1/cosx
cscx = 1/sinx
cotx = cosx/sinx
tan2x = sec2x - 1
sec2x = tan2x + 1
cot2x = csc2x - 1
csc2x = cot2x + 1
第一换元积分法 凑微分 (背
第二换元积分法 换元法 (背
还有直接令的形式,t = 根号下1+e2
分部积分法
比较适用于两类不同函数相乘
- 多项式 与 eax/ sin ax/ cosax,将e和三角函数部分放进dx
- 多项式和lnx / arctanx / arcsinx,把多项式放进dx
- e 与 sinx / cosx
把e放进dx,但是不能一步做出来
三类常见可积函数积分
有理函数积分
分母分解因式,分子分母同乘凑微分
三角有理式积分
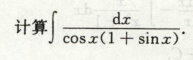
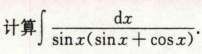
简单无理函数积分
例题
第一换元积分法 凑微分,根号下1-x凑微分
题型:分段函数的原函数应保证在分界点连续
选择题的话,先判断原函数Fx分界点的连续性,再判定F’x=fx
第二换元积分法 换元法
三角函数+指数函数,使用分部积分法,因为分部积分法比较适用于两类不同函数相乘,这里把ex放进dx去
像ex,sinx,cosx好积分的,先凑微分,放进dx
lnx / arctanx / arcsinx这些不好积分的,把多项式放进dx
两类不同函数相乘,使用分布积分,这里先凑1/根号x的微分
这里考点是简单无理函数积分和有理函数积分,直接令根号下多项式 = t
有理函数积分使用拆项的方法做,拆项的具体方法是看出分母是由那两个多项式因子组成的,将分子用这两个多项式因子进行加减运算表示
考点是分部积分和原函数定义和不定积分的性质
常用公式:
∫g(fx) · f‘xdx = ∫g(fx) · 1dfx
考点是换元积分法,综合了不定积分的性质
第五章 定积分与反常积分
定积分的定义
具体定义略,大致说一下是定积分是非均匀分布的闭区间上的求和极限,定积分是一个常数
其中闭区间分成n份,ξi是[xi-1,xi]上的一点,记λ=max{Δxi…}
λ->0可以推出n->无穷,但是n->无穷推不出λ->0
用积分定义做题:
例题:
提出一个1/n,写成lim 1/n[∑f(ξi)]的形式,再写成∫b->a fxdx的形式,其中ξi∈闭区间[a,b]
定积分存在的充分条件
定积分的几何意义
计算面积
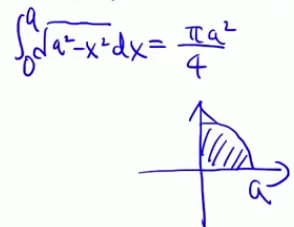
最常见的半圆公式计算定积分的时候
计算偏心圆的定积分
定积分的性质
3)是|a+b| <= |a| + |b|
这个不常用
积分上限的函数 (变上限积分
有点类似于概率论里的分布函数 ∫ fx dx = Fx
本质上是一个函数!
变上限积分定理1
变上限积分定理2
fx为奇函数,它的变上限积分为偶函数
反之,fx为偶,∫0->xfxdx为奇函数
定积分的计算公式
这个最常用啦
换元法
令t=g(x)
x = g-1(t),换dx
t=g(x),换积分上下限
如:
令t=lnx,那么x=et,dx = det
t=lnx,将上下限ab带入lnx,求得新的积分上下限
分部积分
奇偶性
周期性
点火公式
记忆:先写 n-1/n,往后倒推:
写到了2/3就结束
如果写到了1/2,就多乘一个派/2
常用结论
例题
定积分概念例题
考点:定积分定义求极限
提一个1/n出去
写成这个形式
∫上下限a,b 满足 ξi∈[a,b]
下面3题是一个考点
考点:定积分的几何意义
S3注意一下是梯形面积,
f’’x>0表示是函数图像是凹的
考点:定积分的性质,不等式
考点:定积分的几何意义,
变上限积分定理2:fx为奇函数,它的变上限积分为偶函数,反之,fx为偶,∫0->xfxdx为奇函数
这里fx是奇函数,所以Fx是偶函数
上下限a->b,应该满足b>=a的,才有定积分的几何意义,不满足条件需要对调ab,并且添加负号
考点:定积分的几何意义,
这里可以用特殊值法
考点:罗尔定理(F’x = fx,区间连续,端点相等 => 存在fξ=0),
定积分的性质中值定理
中值定理
定积分计算例题
考点:定积分计算之奇偶性
+号拆分成左右两个部分,奇函数部分先化成0,偶函数部分化成2倍
考点:定积分计算之奇偶性,定积分的几何意义
定积分的几何意义,中提到的偏圆公式
考点:定积分常用结论,点火公式,定积分计算之奇偶性
定积分常用结论:
奇偶性,sin2x在[0,Π]上关于Π/2对称
点火公式背一下
考点:第二换元积分法,换元法
考点:换元法,简单无理函数积分
考点:分部积分法,
这里很明显把x放进dx
考点:分部积分法
这里fx是求不出来的,因此只能用分部积分把求fx转换成求f‘x的问题
变上限定积分例题
3种类型,1,23,4
1)这种可以直接求
2)x在变上限定积分里是常数,把x提出去,在对x求导
3)换元,令x-t=u,注意变上下限
4)也是换元,令x+t=u,注意变上下限
考点:变上限积分定理1(就是求导公式)
考点:都是变上限积分求导
这里用的换元法,
但是最快的方法是特殊值法,直接令fx=1
考点:Fx原函数性质(连续,F’x=fx)
因为F‘x=fx在分界点处很难求F’x,
但是通过判断Fx连续性(连续必可导),不连续的直接排除,就可以选出答案了
常用结论:fx不连续,存在跳跃间断点,原函数Fx连续,在间断点处但不可导
考点:定积分的定义
分段函数求原函数,容易做错,类比一下离散型随机变量求分布函数就好,
稍微注意就行
考点:极限计算,洛必达,变上限积分求导
常用结论:
f(x) >0或者f(x)<0,且定积分值=0 => 定积分上下限a=b=0
考点:洛必达,变上限积分求导(或者用定积分性质:中值定理)
之所以可以用定积分性质中值定理,是因为这里被积分式子有fx和gx,可以把fx或者gx提出来变为fξ或者gξ,而ξ->0
考点:微分,隐函数求导,变上限积分求导
隐函数求导注意对x求导时,y是x的函数,y => y’,x·y => y + y’x
反常积分
无穷区间上的反常积分
定义1:(半)无穷区间上[a,正无穷)的反常积分,类似的还有(负无穷,b]无穷区间上的反常积分
这两种无穷区间:一半无穷,一半有界,求它反常积分的散敛性就是直接求定积分,直接带无穷结果是常数则为收敛,若是无穷则为发散
定义2:无穷区间上的散敛性,
这种无穷区间,两端都是无穷,则要拆分成左右两个半无穷区间,两个都收敛,这个无穷区间反常积分才收敛
无界函数的反常积分
无界函数即不是有界函数的函数,如y=1/x
如果函数fx在点a任一领域内都无界,称点a为瑕点,
1/x,在点0处
设函数fx在(a,b]上连续,点a为瑕点,下面极限存在,称此极限为fx在闭区间[a,b]上的反常积分
反之fx在[a,b)上连续,b为瑕点,类比下面极限存在,称此极限为fx在闭区间[a,b]上的反常积分
这种反常积分的散敛性情况,直接计算此极限,若为常数则收敛,若不存在则为发散
函数fx[a,b]上除点c外都连续,c为瑕点,索要计算[a,b]区间上的散敛性,将区间ab拆分成,ac,bc
ac和bc又回到上面所述的反常积分情况,区间ac和bc都收敛,那么ab区间收敛,
只要有一个发散,那么ab发散
反常积分常用结论1 (p积分
反常积分常用结论2
例题
考点:反常定积分的计算
A可以用p积分结论来做,BCD直接计算定积分,若结果为常数则收敛,其实本质上还是考定积分的计算
考点:分段函数的无穷区间上的反常定积分计算
这里的fx是一个分段函数,而要计算分段函数的反常积分,需要拆分成两个部分,1到e和e到正无穷,要求这两个部分都收敛
考点:ex极限计算(左右有别),定积分计算
注意,
第一个0和第二个0代表的正负性是不一样的
考点:同敛性的比较判别法,双瑕端点的散敛性判断
这题要注意,0点是个无界点!所以这个区间ab要拆分成ac和cb,c为了计算方便取1.
同敛性的比较判别法:
现在有∫ab fx dx, ∫ab gx dx,
不失一般性的设a是瑕点,
若有lim x->a (fx/gx) ≠ 0(为非零常数),
那么∫ fx dx,∫ gx dx是同敛性的
计算题,本质还是考定积分的计算。
定积分的计算为非就是3个方法,凑微分,换元和分部积分
这里很明显是两类不同函数相成,用分部积分来做
这题是凑微分,我们一般都会先把e-x消掉
根号一次式,我们直接把令成t,或者另外种方法就是凑根号这个的微分
第六章 定积分的应用
这一章其实很简单,记住4个公式即可
分别是:
平面图形面积公式,
旋转体体积公式,
曲线弧长公式,
旋转体则面积公式
平面图形面积
公式 ∫∫D 1 dσ
图形∈D
1表示高为1,底面积×1 = 体积 = 底面积
dσ是微小块面积,一般为dxdy
常用公式:
旋转体体积
V = ∫∫D 2 × 派 × r(x,y) dσ
图形D围绕直线L:ax+by=c旋转,求体积V
r(x,y)是点xy到直线L的距离 = |ax+by-c|/根号下a方+b方
2派r(x,y)dσ,dσ是图形上一小块,2派r(x,y)则是圆周长,那么圆周长×面积视为圆环体积
这个圆环体积就是体积微分dv
V = ∫∫D dv
记住公式V = ∫∫D 2 × 派 × r(x,y) dσ 即可
但是用的多还是这两个公式:
弧长公式
记住3个,都很类似
旋转体侧面积
绕x轴旋转公式
2派 · fx 是圆周长,圆周长×弧长,视作长条侧面积微分
同理fx可以改成r(x,y)
例题
这部分的例题平面面积计算、旋转体积计算和弧长计算,这部分就直接略了,都是直接套公式的题目,把图形画出来就基本没问题了。
这里我觉得主要难题是在物理应用上,做这种题的主要思想是找微元,像在二维平面建立xy轴,一般就是y做微分,切成许多的横条薄片,这一横条薄片做微元在y上积分
W=F·s,
抽水主要思想是把水沿着y方向,横向划分成n份不同水块,底面积为S,高为dy,抽水就是把这n份水块从底部移动到顶
口,每个水块移动的距离不一样,最后在y上积分即可
这题是考的 压力=压强×面积
水主要思想是把水沿着y方向,横向划分成n份不同水块,单独考虑这一小水块的压力即可
第七章 微分方程
微分方程基本概念
含有位置函数的导数或者微分的方程称为微分方程
微分方程的解是满足方程的函数
积分曲线是方程的一个解在平面上对应的一条曲线
一阶微分方程
5种方法,
可分离变量的方程
这种最简单啦
0次齐次微分方程
这个一般需要提一下东西出来,才能看到y/x,
或者xy需要对调
这个方法的本质是将F(x, y, y’)通过变量代换变成F(x, u, u’)方程
原本的F(x, y, y’)不好用分离变量法,换成F(x, u, u’)就好用分离变量法,求得函数G(u,x) = 0满足方程,u用y/x代回去,变成G(x,y) = 0(或者改写成y=g(x)方程)的方程即为答案,
最后如果有初始条件,计算C即可
一阶线性微分方程
这个就是直接背公式,注意y’前面系数是1
伯努利方程
把yn除过去,会会先一个y1-n,u=y1-n,整理成一阶线性微分方程
全微分方程
可降阶的高阶方程
有3种
F(yn,x) = 0
这个最简单,直接积分即可
F(x, y’, y’’) = 0
令y’=p,y’’=p’,
(这里p’就出现dp/dx)再用可分离变量的方程解法
F(y, y’, y’’) = 0
令y’=p,y’’=p dp/dy
(因为没有x,y’’不能写成dp/dx,要写成dp/dy * dy/dx,即p dp/dy)
再用可分离变量的方程解法
二阶线性微分方程
线性微分方程的解的结构 (理论
相关定理
这个很类似线性代数
很类似线性代数
非齐次方程特解关于非齐次项具有叠加性
二阶常系数齐次线性微分方程
一般形式
y’’ - py’ + qy = 0
先计算特征方程
r1不等于r2 ,er1x,er2x
r1=r2, erx,xerx
r=a加减bi,eaxcosbx,eaxsinbx
例题:
计算特征方程 r1=r2=1/2,erx,xerx
三阶的微分方程怎么算呢?我们发现这个也是常系数微分方程,一样先写特征方程
解一个解是r1=2,将特征方程整理成(r-2)*多项式 = 0,继续解多项式 = 0即可
二阶常系数非齐次线性微分方程
一般形式
如果fx是多项式*指数函数.
那么待定系数,设y* = xk · 多项式 · eλx
其中Qm(x)与fx中的多项式同次.
看λ是特征方程的几重根,
如果λ不是根,k = 0
r1=a,r2=b,λ=a或者=b是一重根,k = 1
r1=r2=c=λ是两重根,k = 2
如果fx是
多项式p1 * 指数函数 eax* 三角函数cosbx +
多项式p2 * 指数函数 eax* 三角函数sinbx
的形式
设y* = xk · eax [多项式 cosbx + 多项式 sinbx]
例题:
欧拉方程
令x=et
y’= dy/dx = dy/dt · dt/dx = dy/dt · 1/x
xy’ = dy/dt
同样可推:
x2y’ = d2y/dt2 -dy/dt
例题
令x=et
原方程就可以写成:
D(D-1)y + 4Dy + 2y = 0
整理得
D2y + 3Dy + 2y = 0
那这个就是二阶常系数微分方程,
算特征方程求r1r2
这里的Dy是y对t求导,因此求出的通解是y=f(t),再换元回来即可。
例题
写在前面:
一阶线性微分方程求解通常有4个思路
- 分离变量
- y/x = u,化成F(u,x)=0的函数,再进行分离变量
- 一阶线性微分方程公式
- 伯努利方程,把yn除过去,令u=y1-n,化成一阶线性微分方程
二阶解法有7个思路
- F(x, y(2+))=0, 直接积分即可
- F(x, y’, y’’) = 0,令y’=p,化成p和x一阶方程
- F(y , y’ , y’’) = 0,令y’=dy/dx=p,把求导的dx消掉,y’’=dp/dx=dp/dy · dy/dx ,化成p和y一阶方程
- 解的结构
- 二阶常系数齐次方程,求特征方程
- 二阶常系数非齐次方程,,先求齐次方程,第二步设特解y*,待定系数
- 欧拉方程,令t=lnx,x2y’’ = D(D-1)y,Dy是y对t求导,D2y是y对t求二阶导
这题考点是0次齐次微分方程求解法
令u=y/x , y=ux
考点:二阶常系数齐次方程
写出特征方程,求出r1r2
考点:微分方程解的结构
y是二阶常系数非齐次线性微分方程的特解,
我们应该记住:
通解y = C1y1 + C2y2 + y*,
重点是找出特解y*,y1和y2是线性无关的函数,
通过y1和y2反推r1r2,找到特征方程,求出a和b
最后通过特解求c
考点:微分方程解的结构,二阶非齐次方程求解
通过齐次方程求得r1r2,找到特征方程,求出a和b
再求解二阶非齐次方程
这里的y* = 多项式为Ax+B,指数函数e0x,λ=0,不是根,所以k=0
考点:微分方程解的结构
y1-y3,y2-y3是齐次方程的解,
这里y1,y2,y3都是特解,y3最简单因此作为y*
通解 = C1(y1-y3) + C2(y2-y3) + y*
综合题
考点:变上限积分求导,一阶线性微分方程求解
考点:切线方程、一阶微分方程求解
第八章 多元函数微分学
这里的微分一般指全微分公式,全微分又需要求偏导数,所以在多元常考微分,就和偏导数一起考了
概念部分常出小题,考点有判断极限存在,求极限,连续性(一般考一元),偏导数定义,二阶偏导数,全微分定义,全微分存在的必要条件和充分条件
第二部分是多元函数微分法,一般称作计算题,这部分题目一般都是方法性的题目,不难,主要掌握3个微分计算方法,
- 直接求偏导
- 公式法 -Fx/Fz
- 两边同时全微分
二元函数基本概念
二元函数极限的定义
动点xy是以任意方式趋向x0,y0的
上3次,下2次,估计为0
做法:取绝对值用夹逼,
0<= |f(x,y)| <= |x|
令y=kx
二元函数的连续性
连续性是一个重极限,是一个区域都连续
一阶偏导数的连续也是一个重极限:
f’x是fx对x求偏导
lim f’x(x,y) = f’x(x0,y0)
因此也是一个区域D都连续,是一个比较充分的条件
偏导数
本质上还是函数的增量与x增量的之比值的极限
求f’x,固定y0
求f’y,固定x0
先代入后求会简化很多很多
f’x几何意义,过点M(x0,y0,f(x0,y0))做平面y=y0与曲面f(x,y)相交,其交线为平面y=y0上的曲线,f‘x(x0,y0)则表示交线在点M处的切线对x轴的斜率
二阶偏导数
二阶偏导数在区域D连续,则下标可以互换位置
全微分
函数的微增量可以写成AΔx + BΔy + o(ρ)的形式,其中A=f’x,B=f’y,是x和y的偏导数,
ρ是动点到定点的距离
因此全微分的必要条件是f’x和f’y存在(为常数)
因此不可导肯定不可微
如何证明可微性?
- 求出f’x, f’y
- 证明lim {Δz - [ AΔx + BΔy] } / o(ρ) = 0
其中Δz = f(x0+Δx, y0+Δy) - f(x0, y0)
全微分存在的充分条件
一阶偏导数存在且连续
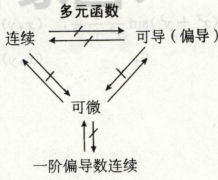
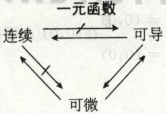
连续、可导、可微之间的关系
多元函数和一元函数的区别主要是偏导引起的
类比一下一元函数
例题 (全微分定义和性质
xy/x2+y2这个是很常见的不连续
可导性需要用偏导的定义来求f’x, f’y,直接看这个极限存不存在即可
这题个人认为是一道难题,需要重点掌握全微分的定义,看出分母部分是动点到定点的距离,分子部分需要凑一个f(x0, y0),凑成形式:Δz - [AΔx + BΔy],那A和B就是f’x和f’y
另外一个解题思路是特殊值法,令fxy = 2x-y+2
多元函数微分法
这部分主要就是计算啦
复合函数链导法
我更喜欢叫走路法 doge
全微分形式不变性
这部分的考题还不是很清楚
隐函数求导
3个方法
- 直接对方程左右两边求x的偏导,y要视为x的函数
- 公式法 dy/dx = -Fx/Fy
- 全微分法,方程左右两边每一项同时求全微分,整理dy和dx,得出dy/dx
直接对x求导,y和z都视为x的函数,
而公式法一般用在F(x,y,z)=0的情况,求F’x时,y和z都作为常数
数一额外要求
例题 (微分法
这部分例题比较容易,但是要细心,对f’1求导时 先把f’1(u,v)写在旁边,对着来求导,就没那么容易错。
这题建议是先代入y后求导
就是直接求,先代入后求导,解1这样做就慢了
考点:二阶微分方程和二阶偏导数
例题 (隐函数
隐函数就3个方法
常用的是前2个,
直接方程两边对x求偏导,y和z都看作是x的函数
公式法,求F‘x,一般公式法是用在F(x,y,z)=0的情况,求F’x时,y和z都作为常数
多元函数的极值与最值
可能的极值点:
- 驻点
- f’x,f’y至少一个不存在的点
首先要求f(x,y)可导,f’x=0 f’y=0称为 驻点
极值的定义
我们可以看到要有极值,首先就是该点领域附近有定义,所以端点是取不到极值的,只能取到最值
极值的必要条件
f’x = 0
f’y = 0
无约束极值
存在充分条件
一般的,我们能够计算f’x=0,f’y=0,我们希望进一步判断是极大值还是极小值
用此条件判断需要f(x,y)在某领域内有二阶连续偏导数
记A=f’xx,B=f’xy, C=f’yy
计算AC-B2,判别式大于0,A>0 开口朝上 有极小值,A<0 开口朝下,有极大值
注意:
对于1)来说还有一个函数可以用定义来判定,如 f(x,y) = x2y2,在0,0点一定是极小值
条件极值
什么是条件极值?条件极值是求在g(x,y)=0的条件函数fxy的极值
方法为拉格朗日乘数法
这里问题的关键是如何解方程组,一般情况下λ=0或者什么=0,分情况讨论
核心思想还是消元
注意:
其实就结果直接计算,选最大做极大值,选最小的做极小值
最大值和最小值
3步
- 求极值
求f’x f’x,求ABC,或者用拉格朗日乘数法 - 求边界上点的极大值和极小值
这里的边界一般就作为条件函数,化成Gxy=0 用拉格朗日乘数 - 比较
例题
这一题给了函数的全微分,全微分说明该函数可导且连续,下面要求该点是极大值还是极小值,第一个思路就是求ABC,因为f’x,f’y已经知道了,ABC很好求
第二个思路是直接构造特殊值,凑微分,求出z=f(x,y)
这题直接让我求极值,不难,求f’x=0,f’y=0,ABC就行
这题就是直接考拉格朗日乘数法多元推,难点在怎么解方程组,其实也很好解
这里给了全微分,和初始条件,直接用凑微分法求出原函数,
我要们求最值,需要求两个,1是极值,2是边界上的点,求边界上的最值有两个思路:
- 化条件为无条件,y用x表示,或者用参数方程表示y和x
- 条件用拉格朗日乘数法
第九章 二重积分
这部分可能会考大题
二重积分的概念
积分微元是平面上的小块 dσ
定义
几何意义
曲顶柱体的体积
性质
- 不等式性质
- 中值定理
二重积分的计算
1)直角坐标系 xy,yx,或者交换次序
2)极坐标
3) 利用奇偶性
4) 轮换对称性
区域D如果x,y互换,区域D不变,那么则有∫∫ f(x) dσ = ∫∫ f(y) dσ
例题
这部分主要就是考交换积分次序和计算,
解法很固定,都是先画图,然后选择4种计算方法
直接做不好做,交换积次序
极坐标计算
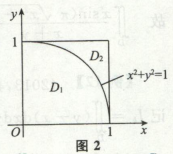
这题考的奇偶性,画出图形,是一个三角形,主要思想就是通过添加辅助线,将图形划分为两个关于x和y轴对称的图形,利用奇函数性质化简
奇函数性质化简,画出图像,使用极坐标,注意三角函数部分的化简,点火公式运用
绝对值的处理,划分区域成D1,D2,D2计算可以用正方形-D1
这题第一个想法是用极坐标计算,但是分子一个x不好计算,
又发现区域D是一个圆,考虑轮换对称性,加一个f(y,x)
将分母的x+y消掉
方法二,直接计算
技巧:
θ=Π/2 - t
在三角函数里,利用
区间不动的变量代换: 令x=a+b-t
再利用诱导公式,cos转换成sin,相加进行化简
有点像轮换对称性的思想
考点是二重积分的几何意,在y-x>0区域D种, ∫∫ y-x dσ >0,
这题是函数fxy不变在不同区域种,
另一种考法是不等式性质,在区域D不变,考虑不同的fxy
第十章 无穷级数
常数项级数
什么是常数项级数
就是每一项都是常数的无穷项累加
主要考点在敛散判断,
发散通常就是S = 无穷
直接展开计算
等比数列求和,有公式
性质
- 级数S收敛,kS也收敛
- 级数u和级数v收敛,u+v也收敛
- 不存在 + 存在 = 不存在
- 不存在+ 不存在 = 不确定
注意
级数的敛散性只与后无穷项有关
收敛级数加括号收敛且和不变
级数加括号收敛,原级数不一定收敛,如 1-1+1-1…
级数加括号后发散,原级数一定发散,部分发散,整体一定发散
级数收敛的必要条件
对1举个反例,如1/n的级数发散,但是极限lim un = 0
常数项级数审敛准则
3类审敛法
这部分考题的重点,分成3个部分,
1)是正项级数,就是每一项都大于0,
有4个办法,先用34,比值法和根值法,再用12比较判别法和比较法的极限形式(需要缩放,不好做)
34方法的思想是等比数列的类比
12方法,大收小也收,小散大就散,2和1差不多意思,(2)的①同敛散转换用的挺多
常用的缩放结论:
p级数
1/n发散很经典
等比求和
2)交错级数,就是一个正数,一个负数,交错的级数,
用莱布尼茨准则,数列单调 且 lim un=0,则交错级数收敛
注意反之不成立
3)任意项级数
用加绝对值的方法,转换成正项级数,若绝对值|S|收敛,则S必收敛,因为大收敛小必收敛
或者利用条件收敛,条件收敛的正/负项构成的级数一定发散,
这是因为S收敛了,而|S|发散,一种特殊情况是S是一正一负抵消了,单独把正项和负项提出来则必发散
推导:un±|un| => 收敛±发散 = 发散
例题
A) an=bn是一个交错级数 -1n/√n, anbn = 1/n发散
B) an=bn=1/n, anbn = 1/n2 收敛
C)正确
∑|bn|收敛,lim an=0,an有界,|an| <= M,
|anbn| <= M|bn|, M|bn|收敛,则|anbn|收敛
∑|an|收敛,正项级数收敛,则lim |an| -> 0(0 <=lim |an|< 1),
an2 <= |an|,则∑an2收敛
有两个结论,
∑|bn|收敛,lim an ->0,则∑|anbn|收敛
∑|an|收敛,则 ∑an2收敛
D)an=bn=1/n,an2bn2收敛
A 正确定理,级数收敛,级数加括号也收敛,反之不成立,BD错误
C,un若为交错级数前项加后项抵消,改成减必发散
幂级数
定义
什么是幂级数?
类比一下泰勒展开,泰勒展开最后高阶无穷小代替,而幂级数是n->无穷的累加和
幂级数定理
1) 阿贝尔定理
幂级数S(x)的收敛半径和收敛域的由来
2)幂级数收敛性质只有下面三种可
收敛半径、收敛区间和收敛域
注意:
条件收敛则一定是收敛区间的一个端点,刚好是一个临界状态,∑anxn收敛,∑|anxn|发
求收敛半径的两个方法,比值法和根值法,这和?什么很像
幂级数性质
1)有理运算性质:加减乘除
R是R1R2中小的那个
anxn·bnxn的系数是有规律的,注意xn的系数:a的i从0到n,b的j从n到0,aibj累加
分析性质,
连续性:收敛区间内连续
可导性和可积性:级数项乘一个或者除一个数不影响收敛区间
例题
求收敛半径就两个求法,比值和根值,注意使用系数算
要求收敛区间,先求收敛半径,收敛区间=(x0-R,x0+R)
难点:判断端点处,x=常数R,变成常数项级数,判断的收敛性,用3类审敛法(正项,交错,任意)
系数一样中心不一样 => 收敛半径一样,收敛域平移
这题考的是阿贝尔定理和收敛域平移
破题关键在于:幂级数定理(条件收敛的临界状态),还有一个思想要掌握是幂级数在x=x0处是常数项级数
级数an在x=1时条件收敛,则an(x-1)在x=2的时候条件收敛,则2是一个端点,x=1又是中心,可以求出收敛区间(0,2)
函数的幂级数展开
定义
函数表示成幂级数形式,一种趋近的思想,化曲为直
展开幂级数的两种方法:
直接法,用下面的定义
间接法,用7个常用公式去凑
幂级数展开的必要条件是fx任意阶可导,
展开中心x0的改变会改变收敛区间,展开中心与收敛半径的关系为(x0-R,x0+R)
定理
展开式唯一
泰勒级数
这个其实就是泰勒公式,很熟悉的形式
fx任意阶可导 => 泰勒级数在收敛区间内收敛与fx 【充要条件】是 lim Rn = 0
常用展开式(背
例题(幂级数展开
分母因式分解,1/2-x的处理是提一个1/2 分母化成1-x的形式
老样子,分母因式分解拆项,分母提项化成 1/1±x的形式
求导数的级数展开,在积分
例题(级数求和
求收敛域,先求半径,判断端点
已有公式1/1-x转换=∑xn,原式 = x∑nxn-1,x∑(xn)’
已有公式 1/1+x = (-1)n-1 xn
分母拆项,
常用结论: ∑xn/n = - ln(1-x)

S‘x求积分Sx是变上限积分∫x->0 S’t dt
傅里叶级数
傅里叶级数主要研究周期函数,fx用级数来表示
主要记住an bn和傅里叶级数的写法
an和bn就只差了cos和sin,a是cos,b是sin
狄利克雷收敛定理
fx在[-pai,pai]连续且只有有限个第一类间断点,且最多只有有限个极值点,则fx在区间里处处收敛。且有3个收敛公式:连续点,间断点,端点
函数展开公式
周期2Π省略,l改成Π即可
用到了积分性质的奇偶性
奇延拓和偶延拓
例题(狄利克雷收敛定理
狄利克雷收敛定理,1是端点,S(1)收敛于f(-1+)+f(1-)/2
函数展开只有bn,an = ∫ fxcosnx = 0,说明fx是奇函数,Sx从题也可以看出是奇函数,S(-1/2) = -S(1/2),用狄利克雷收敛定理Sx=fx
例题(函数展开傅里叶级数
周期为2,2l=2,l=1,
函数在区间上连续,且为偶函数,
求an、a0即可,bn=0,根据定义写出傅里叶级数
fx写成傅里叶级数,当x=x0时化成某些特殊的常数项级数
展开3部分走,
定周期T=2l,确定l,
求an、a0、bn
写级数展开
这里还考了奇偶延拓,展开成余弦,说明fx是偶函数,偶延拓
第十一章 向量代数与空间解析几何及多元微分学在几何上的应用
向量代数
这部分比较简单,主要记住点乘和叉乘的公式,还有几何意义
点乘
余弦公式推导和垂直
叉乘
叉乘是一个向量
叉乘求出来的向量同时垂直被计算的两个向量
平行则叉乘=0
a×a=0,b×b=0
性质
(a×b) · a = 0
(a×b) · b = 0
混合积
混合积=先叉乘再点乘,代数上等于求行列式,
轮换对称性和交换变号,其实就是行列式的性质
例题(向量代数
空间平面与直线
主要还是记住公式
点到直线距离,用叉乘的模的几何意义
例题
比较简单了,略吧
曲面与空间曲线
线段绕轴旋转形成的面的方程
柱面方程,核心思想就是消掉一个变量,比如z
常见的二次曲面,知道图像
空间曲线投影,先求柱面,再z=0
例题(曲面与空间曲线
求平行z轴的柱面,联立消去z即可
曲线绕轴旋转,绕什么轴,那个字母不动,另一个字母换成√另两个字母的平方合
求曲线在面上的投影,先消元,投影到xoy面上,消去z,投影到xoz面上,消去y
多元微分学在几何上的应用
曲面的法向量
到了曲线上求的就是切向量了
例题
在点(0,1,-1)处,可以通过F’x F‘y F’z求法向量,再用点法式求切平面
绕y轴旋转,y不变,x变换,求的F’xF’yF’z
面与面平行,则它们的法向量平行,求出切点,代回求得法向量,点法式求平面
第十二章 多元积分学及其应用
三重积分
计算:
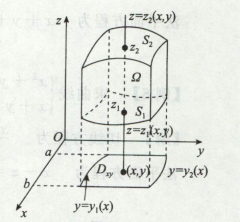
1)直角坐标,先1后2,
先2后1,
如果fxyz只有z,后面积分部就计算横截面积
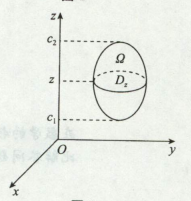
柱坐标,
适合范围,
fxyz = gz · h(√x2+y2) = gz · h(ρ)
利用奇偶性
还有轮换对称性
例题
利用轮换对称性
主要是能画出图像,第一个是圆锥面,第二个柱面
曲线积分
第一类线积分
对弧积分
性质:积分路径与结果无关
计算:
1)直接法:
直接把弧微分展开,常用参数方程(极坐标)
2)利用轮换对称性
3)利用奇偶性
第二类线积分
两类线的联系
对x、y等垂直方向积分,
计算:
曲线封闭吗?是,green公式,积分路径无关吗?否,参数方程(极坐标)或者补线用green
直接法,用参数方程x、y都换成一个t,对t积分
green公式
逆时针正向,顺时针要加负号
积分路径无关
斯托克斯公式(空间
例题
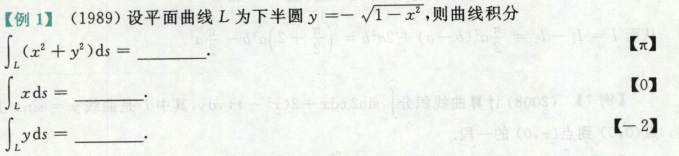
x奇函数,图像关于y对称,
利用参数方程计算
用参数方程好点
曲面积分
第一类面积分
性质:与方向无关
计算
也是直接法、奇偶性、轮换对称性
Dxy是投影域,扁平到平面中,函数×曲线翘值
第二类面积分
和第一类线积分相似
上为正
计算
直接法,把z换成xy的表达,投影成二元的平面积分
高斯公式
变成空间三重积分,要求分片光滑封闭空间曲面
例题
一类面积分,直接法,利用公式即可,
变成投影域的二重积分,被积项=函数×曲面翘值
关键:
- 找好投影
- 计算dS=√1+z’x2+z’y2 dxdy
这题一看就是利用高斯公式好点,补一个面
多份积分应用
补充形心,是ρ视为1常数的特殊质心
记住第二列即可,其他列可以推导
关键是写出F的向量,这是一个二类线积分
二类面积分问题
例题:
形心,ρ视为1常数的特殊质心
场论初步
方向导数
计算用定理,
注意这里的cos是【l向量】 的方向余弦,要单位化
梯度
就是这点的切线
散度和旋度
要求会计算即可
例题:
用方向导数定理(定义不好做),再用拉格朗日乘数法计算最值
方向导数 = u’xcosa + u’ycosb + u’zcosc,
cos是l的方向余弦
梯度是一个向量,定义:(f’x i,f’y j , f’z k),
依次计算f’x y z即可
直接套公式
算术边角料:
x1/2 * x1/3 = x5/6,不是x1/4和x1/5
cos2x=cos²x-sin²x =2cos²x-1 =1-2sin²x